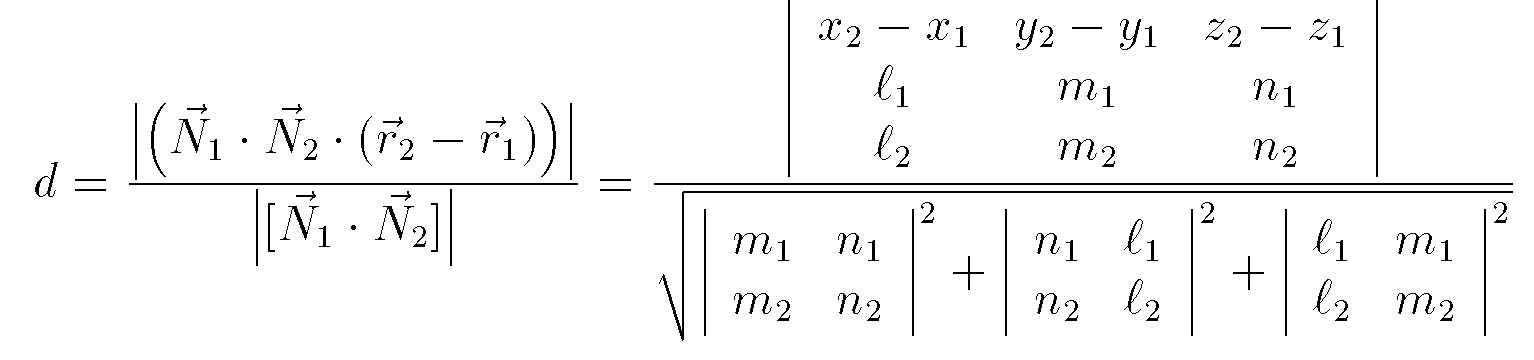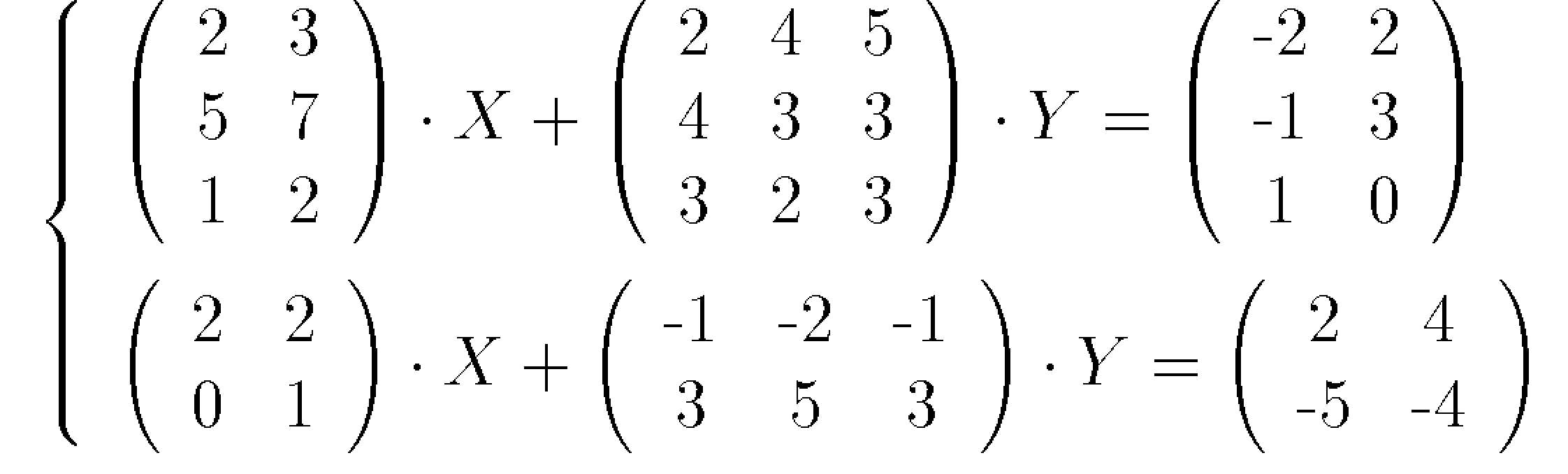
$$
\left\{\begin{array}{l}
\left(\begin{array}{cc}2 & 3\\5 & 7\\1
& 2\end{array}\right)\cdot X+
\left(\begin{array}{ccc}2 & 4 & 5\\4
& 3 & 3\\3 & 2 & 3\end{array}\right)\cdot Y=
\left(\begin{array}{cc}\mbox{-}2 & 2\\ \mbox{-}1
& 3\\1 & 0\end{array}\right)\\[7mm]
\left(\begin{array}{cc}2 & 2\\0 & 1\end{array}\right)\cdot
X+
\left(\begin{array}{ccc}\mbox{-}1 & \mbox{-}2
& \mbox{-}1\\3 & 5 & 3\end{array}\right)\cdot Y=
\left(\begin{array}{cc}2 & 4\\ \mbox{-}5
& \mbox{-}4\end{array}\right)
\end{array}\right.
$$
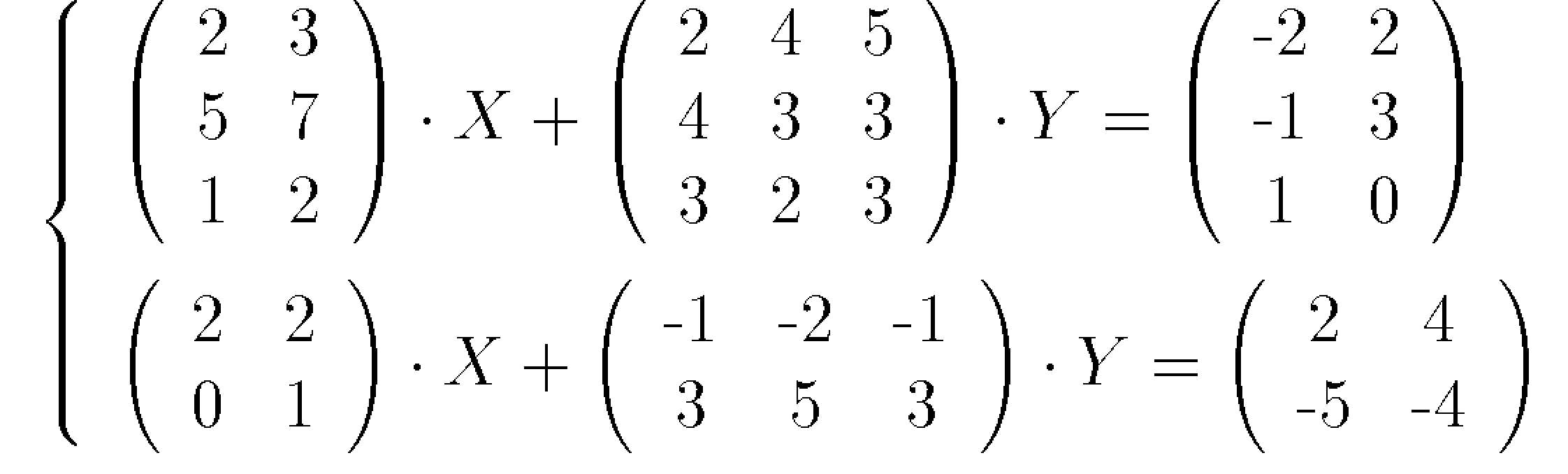
Æèøýý ¹2
$$
P{=}\arraycolsep=0.15em\left(\begin{array}{ccccccccc}
1 &&&&&&&&\\[-3mm]
& \ddots & & \vdots & & \vdots
&&&\\[-2mm]
&&1 &&&&&&\\[-1mm]
&\dots&&0 & \dots & 1 &
& \dots\\[-2mm]
&&&\vdots & \ddots & \vdots
\\[-1mm]
& \dots &&1 & \dots & 0 &&\dots\\[-1mm]
&&&&&& 1 \\[-2mm]
&&&\vdots &&\vdots &&\ddots\\[-3mm]
&&&&&&&&1
\end{array}\right)\begin{array}{l}(i)\\[4mm](j)\end{array}
\hspace{2cm} Q{=}\left(\begin{array}{ccccccc}
1 &&&&&&\\[-3mm]
& \ddots & \vdots & & \vdots
&&\\[-1mm]
&\dots&1 & \dots & \alpha &
\dots\\[-1mm]
&&\vdots & \ddots & \vdots \\[-1mm]
& \dots &0 & \dots & 1 &\dots\\[-1mm]
&&\vdots &&\vdots &\ddots\\[-1mm]
&&&&&&1
\end{array}\right)\begin{array}{l}(i)\\[5mm](j)\end{array}
$$
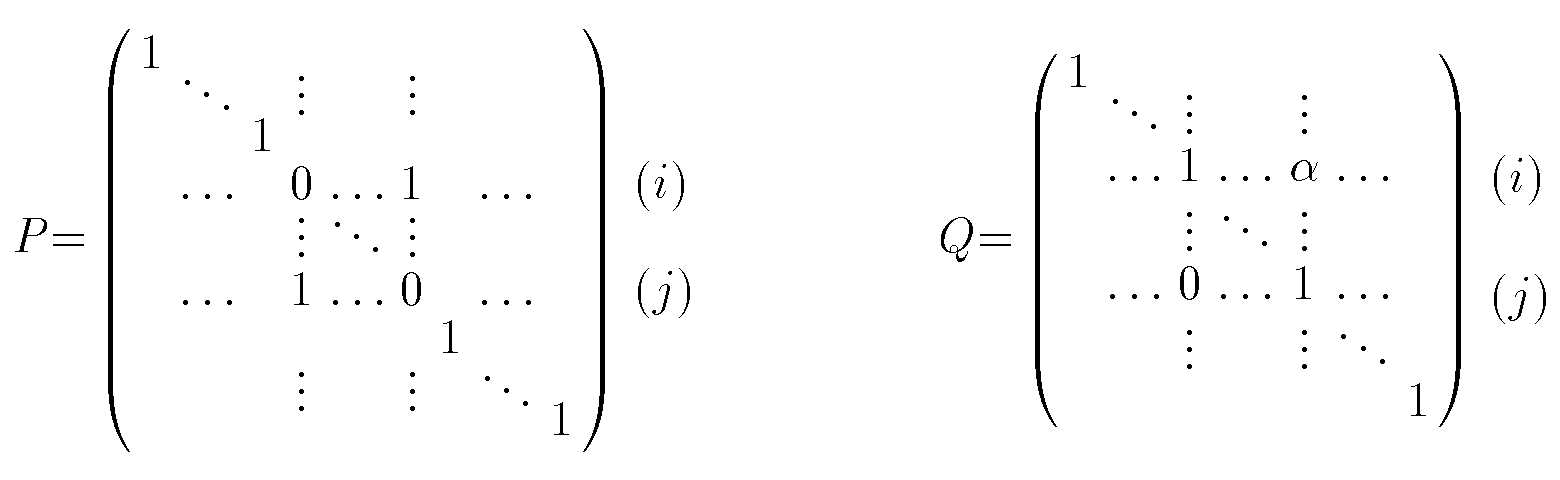
Æèøýý ¹3
$$
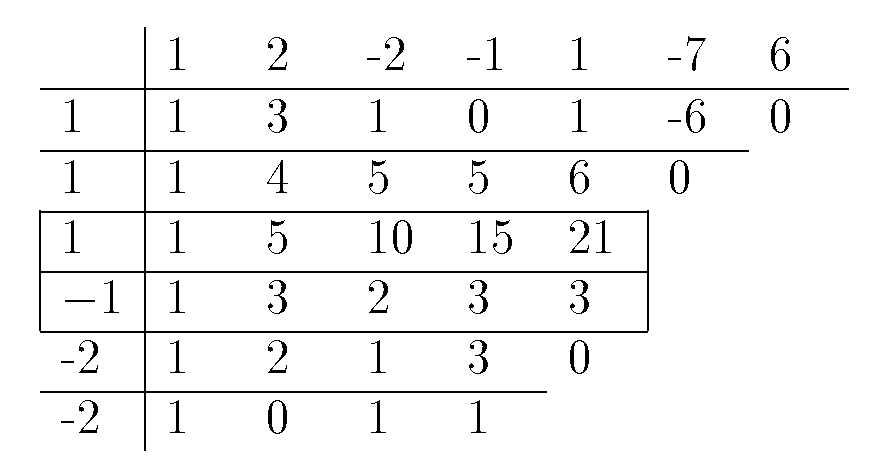
\begin{array}{p{5mm}|p{5mm}p{5mm}p{5mm}p{5mm}p{5mm}p{5mm}p{5mm}}
& 1 & 2 & -2 & -1 &
1 & -7 & 6\\ \hline
1 & 1 & 3 & 1 & 0 & 1 &
-6 & 0\\ \cline{1-7}
1 & 1 & 4 & 5 & 5 & 6 &
0\\ \cline{1-6}
\multicolumn{1}{|l|}{1} & 1 & 5 &
10 & 15 & \multicolumn{1}{l|}{21}\\ \cline{1-6}
\multicolumn{1}{|l|}{-1} & 1 & 3 &
2 & 3 & \multicolumn{1}{l|}{3}\\ \cline{1-6}
-2 & 1 & 2 & 1 & 3 & 0\\
\cline{1-5}
-2 & 1 & 0 & 1 & 1
\end{array}
$$
Æèøýý ¹4
$$
\arraycolsep=.1em\begin{array}{crcrcrcrc|cl}
~ & 5x^3 & + & 12x^2 & - &
7x & + & 34 & ~ & ~ & x^2-x+2\\\cline{1-1}\cline{10-11}
& 5x^3 & - & 5x^2 & + &
10x & & & & & 5x+17\\\cline{2-8}
& & & 17x^2 &
- & 17x & + & 34\\\cline{3-3}
& & & 17x^2 &
- & 17x & + & 34\\\cline{4-8}
& & & &
& & 0 & \multicolumn{4}{l}{=r_3(x)}
\end{array}
$$
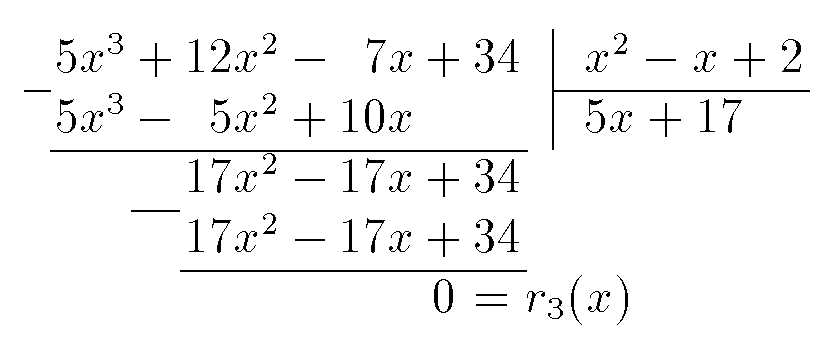
Æèøýý ¹5
$$
\left.\begin{array}{r|l}
x^6 & a+d=0\\
x^5 & -4a+b+e-3d=0\\
x^4 & -4b+c-3e+k=0\\
x^3 & -4c+d+m-3k=0\\
x^2 & a+e-3m=0\\
x & b+k=0\\
x^0 & c+m=1
\end{array}\right\}\Rightarrow\hspace{-2mm}\begin{array}{l}
~~~~a ~~ b ~~ c ~~ d ~~ e ~~ k ~~ m\\
\arraycolsep=0.2em
\left(\begin{array}{ccccccc|r}
1 & 0 & 0 & 1 & 0 & 0 &
0 & ~0\\
\mb{-}4 & 1 & 0 & \mb{-}3 & 1
& 0 & 0 & 0\\
0 & \mb{-}4 & 1 & 0 & \mb{-}3
& 1 & 0 & 0\\
0 & 0 & \mb{-}4 & 1 & 0 &
\mb{-}3 & 1 & 0\\
1 & 0 & 0 & 0 & 1 & 0 &
\mb{-}3 & 0\\
0 & 1 & 0 & 0 & 0 & 1 &
0 & 0\\
0 & 0 & 1 & 0 & 0 & 0 &
1 & 1
\end{array}\right)\end{array}\sim
$$
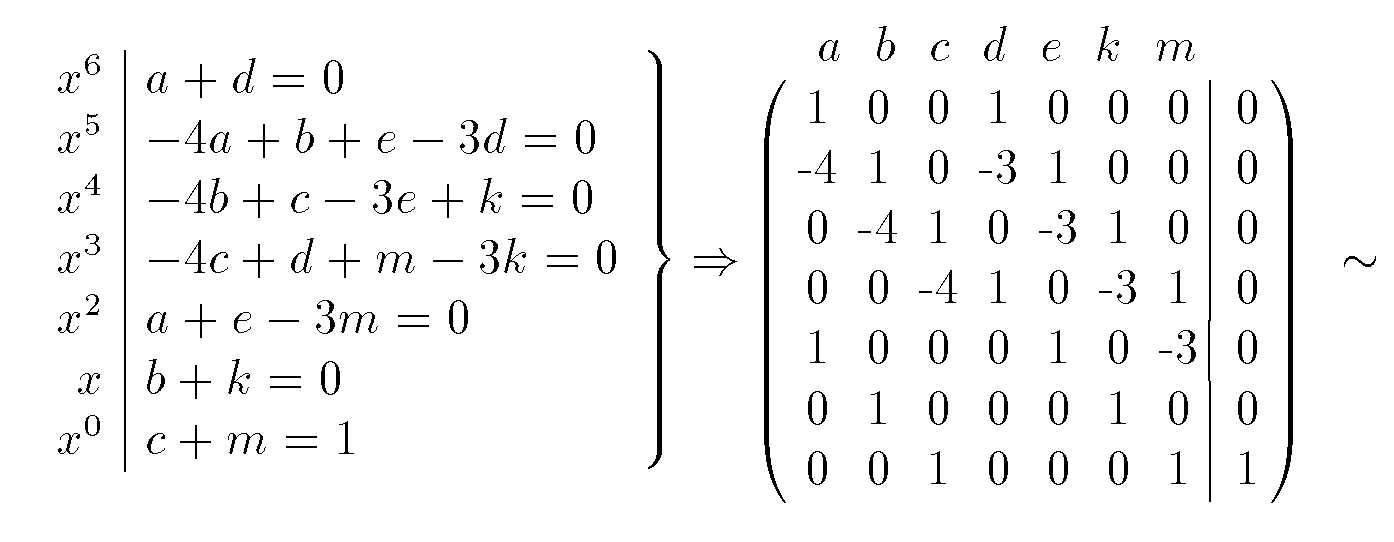
Æèøýý ¹6
$
\displaystyle\lim_{x\to0}\frac{\sin\alpha x}{\sin\beta
x}=
\frac{\displaystyle \lim_{x\to0}\frac{\alpha
x\sin\alpha x}{\alpha x}
}{\displaystyle \lim_{x\to0}\frac{\beta x\sin\beta
x}{\beta x}}=\frac{\alpha}{\beta}
$
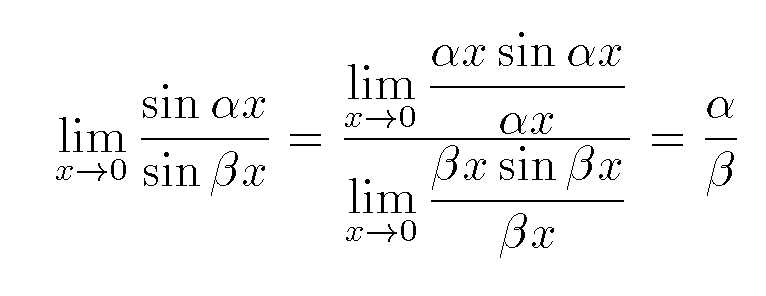
Æèøýý ¹7
$
\displaystyle\int\limits_0^{+\infty}\frac{\displaystyle\left(
\frac{\ln(1+x^2)}{\sin^22x+\cos2x}+e^{2x}\sin^2x\right)
}{\displaystyle\frac{\sqrt[3]{\arctg x+1}}{1+x^2}}dx
$
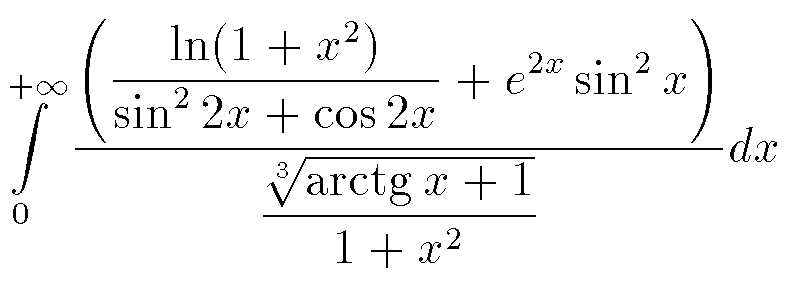
Æèøýý ¹8
$$
d=\frac{\Bigl|\Bigl(\vec N_1\cdot\vec N_2\cdot(\vec
r_2-\vec r_1)\Bigr)\Bigr|}{\Bigl|[\vec N_1\cdot\vec N_2]\Bigr|}=
\frac{\left|\begin{array}{ccc}
x_2-x_1 & y_2-y_1 & z_2-z_1\\
\ell_1 & m_1 & n_1\\
\ell_2 & m_2 & n_2
\end{array}\right|}{\sqrt{
\left|\begin{array}{cc}m_1 & n_1\\m_2 &
n_2\end{array}\right|^2+
\left|\begin{array}{cc}n_1 & \ell_1\\n_2
& \ell_2\end{array}\right|^2+
\left|\begin{array}{cc}\ell_1 & m_1\\\ell_2
& m_2\end{array}\right|^2}}
$$